A primer on differential geometry and dynamics. Including many thoughts and musings on the geometry of motion.

Hamiltonian Dynamics

Let us begin with a smooth manifold $X$ which we will call the configuration space. An exmaples is like this spring mass system $X = (\mathbb{R}, q)$.

An example of a simple configuration.

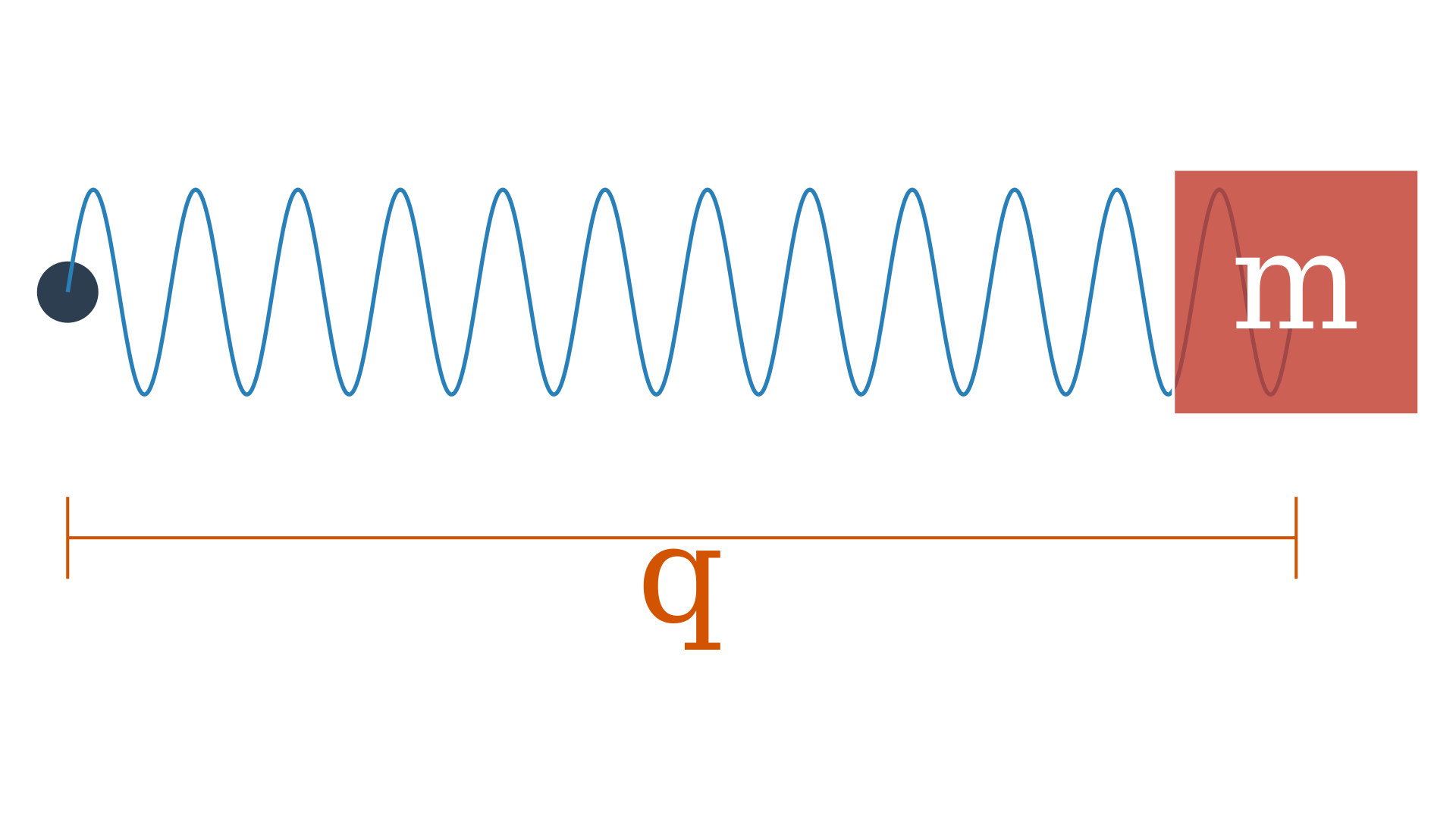
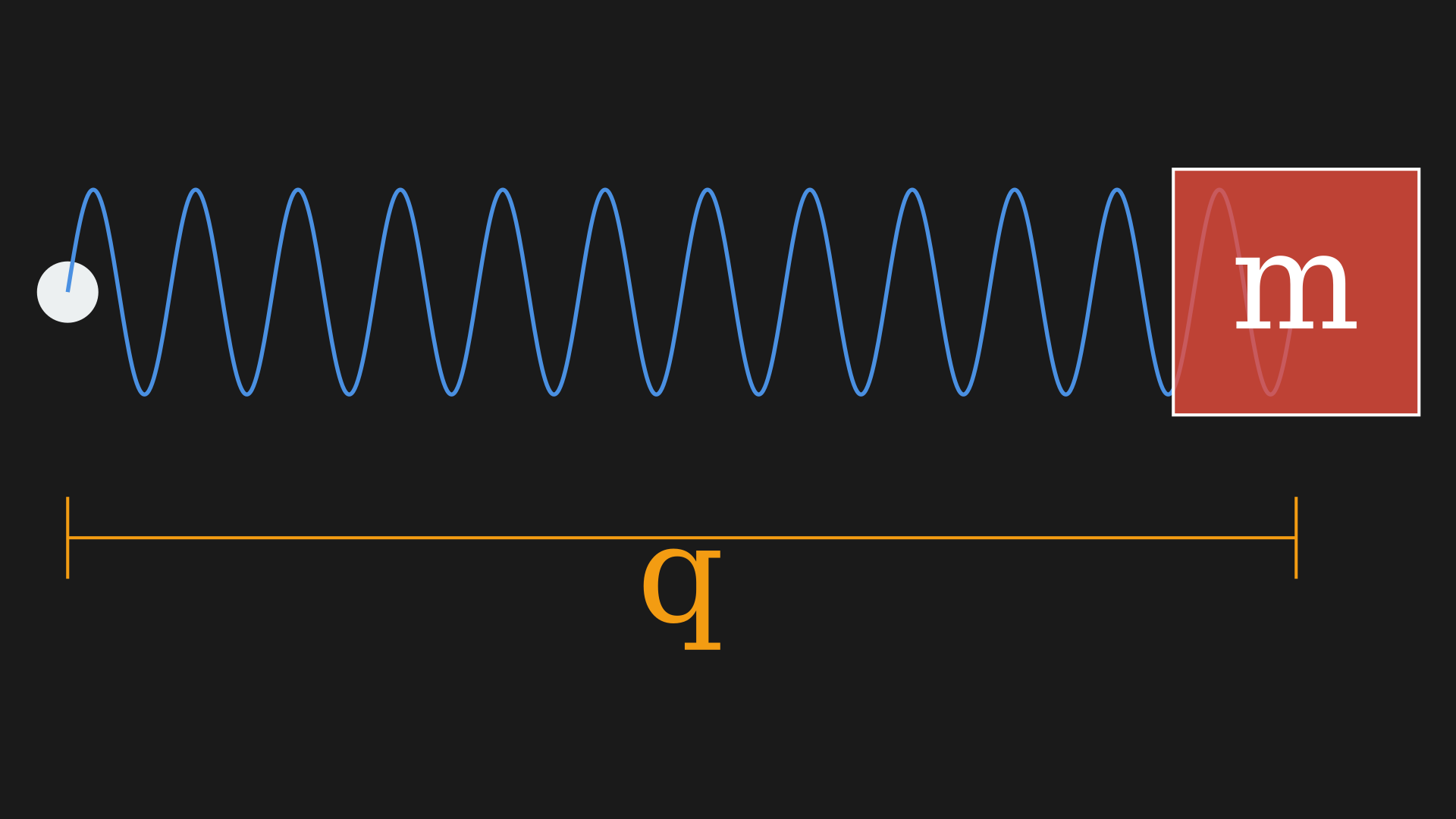
The position of the mass is a configuration which forms a smooth manifold in one dimension. We could also have, this in multiple dimensions, $X = (\mathbb{R}^n, (q_1, q_2, \ldots, q_n))$ or the set of complext numbers with norm of one $X = S^1 = \lbrace z \in \mathbb{C} : \mid z \mid = 1 \rbrace $ or the $n$-sphere inside the $n+1$-dimensional space $X = S^n \in \mathbb{R}^{n+1} \quad S^n = \lbrace (q^0, q^1, \ldots, q^n) \in \mathbb{R}^{n+1} : \sum_{i=0}^n (q^i)^2 = 1 \rbrace $. These configurations are like point particles moving in the smooth manifold.

Broadly speaking, the entire purpose of Hamiltonian mechanics is to predict the future or past of a system based on the current state of the system, so if we know some initial state of the system fully and we know the law that it satisfies we can predict the future or past. Generally speaking, the future is not just defined by the the current “position” or configuration but rather it is uniquely determined by the state of the system. This state consists of $q$: the position and $p$: the momentum. This state is an element of the set which is the cotangent bundle $T^*X$ (the state space or phase space), $(q, p) \in T^*X$. This cotangent bundle is essentially the set of all possible states of the system, $q \in X$, and $p$ is an element in the dual space of the tangent space to $Q$ of $X$ $p \in T_q^*X$. The momentum $p$ is a covector at $q$. This essentally tells us how much momentum there is in a direction $v \in T_qX$.

Momentum is a covector at the point $q$.

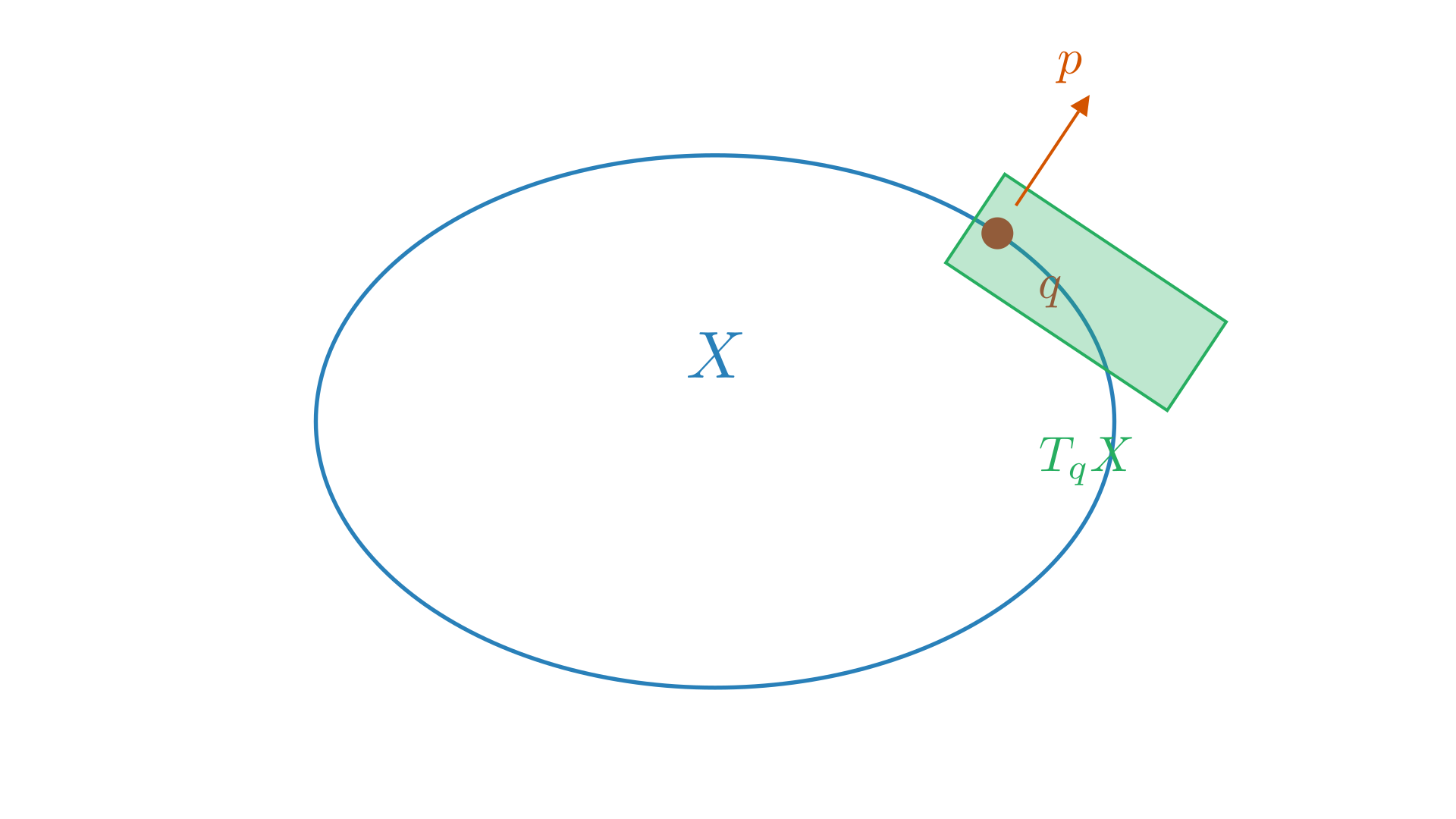
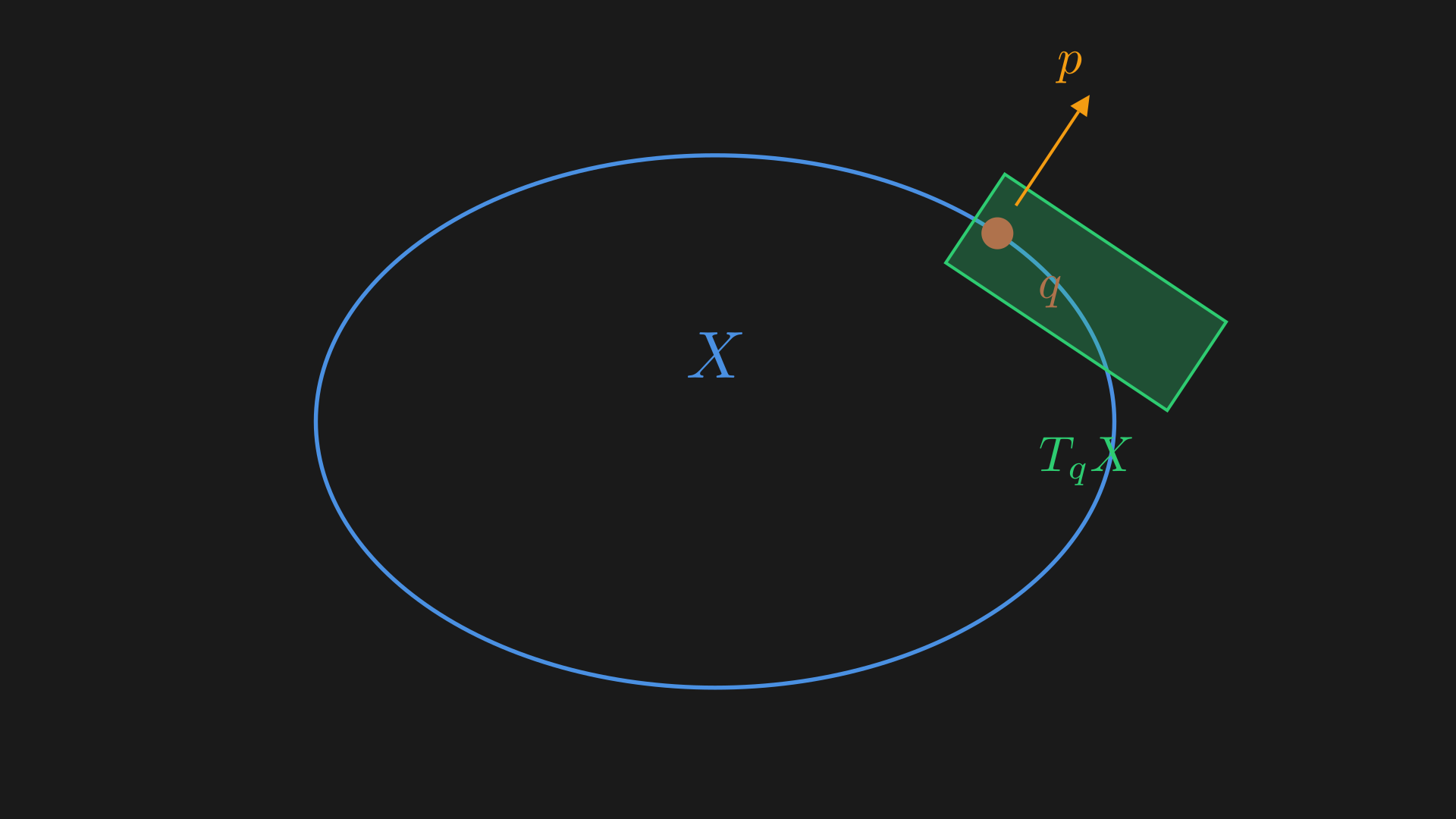
A tangent vector at $q \in X$ can be written as,

\begin{equation} v = \overbrace{v^1}^{\text{components}} \underbrace{\frac{\partial}{\partial q^1}}_{\text{vector field}} + \overbrace{v^2}^{\in \mathbb{R}^n} \frac{\partial}{\partial q^2} + \cdots + v^n \frac{\partial}{\partial q^n}. \label{eq:tangent-vector} \end{equation}

The $\frac{\partial}{\partial q^i}$ represents the vector fields which lives in the $n$-dimensional space and points in $q^i$ direction.

A cotangent vector at $q \in X$ can be written as,

\begin{equation} p = \overbrace{p_1}^{\text{components}} \underbrace{dq^1}_{\text{dual basis}} + p_2 dq^2 + \cdots + p_n dq^n. \label{eq:cotangent-vector} \end{equation}

And since it is a dual basis evaluating the vector field $\frac{\partial}{\partial q^i}$ at $dq^i$ gives us $1$ and at any other $dq^j$ gives us $0$. Essentially by choosing the co-ordinates $(q^1, q^2, \ldots, q^n)$ we automatically obtain for co-ordinates $(q^1, q^2, \ldots, q^n, p_1, p_2, \ldots, p_n)$ for $T^*X$ (cotangent bundle) which is a $2n$-dimensional smooth manifold. The $(p_1, p_2, \ldots, p_n)$ are called the canonical conjugate variables of $(q^1, q^2, \ldots, q^n)$.

(Main Idea). The evolution in time of the state $(q, p) \in T^*X$ is the flow of a vector field on $T^*X$.

This means if $X=S^1$ then the cotangent bandle of $S^1$, $T^*S^1$ contains a bunch of vector spaces, one ofor every point on $S^1$. This is because we know for every point on $S^1$ there is a tangent space which is a line or 1-dimensional space and the dual space to that is 1-dimensional space. The $T^*S^1$ is $S^1 \times \mathbb{R}$ which is a cylinder.

The cotangent bundle of $S^1$ is a cylinder.

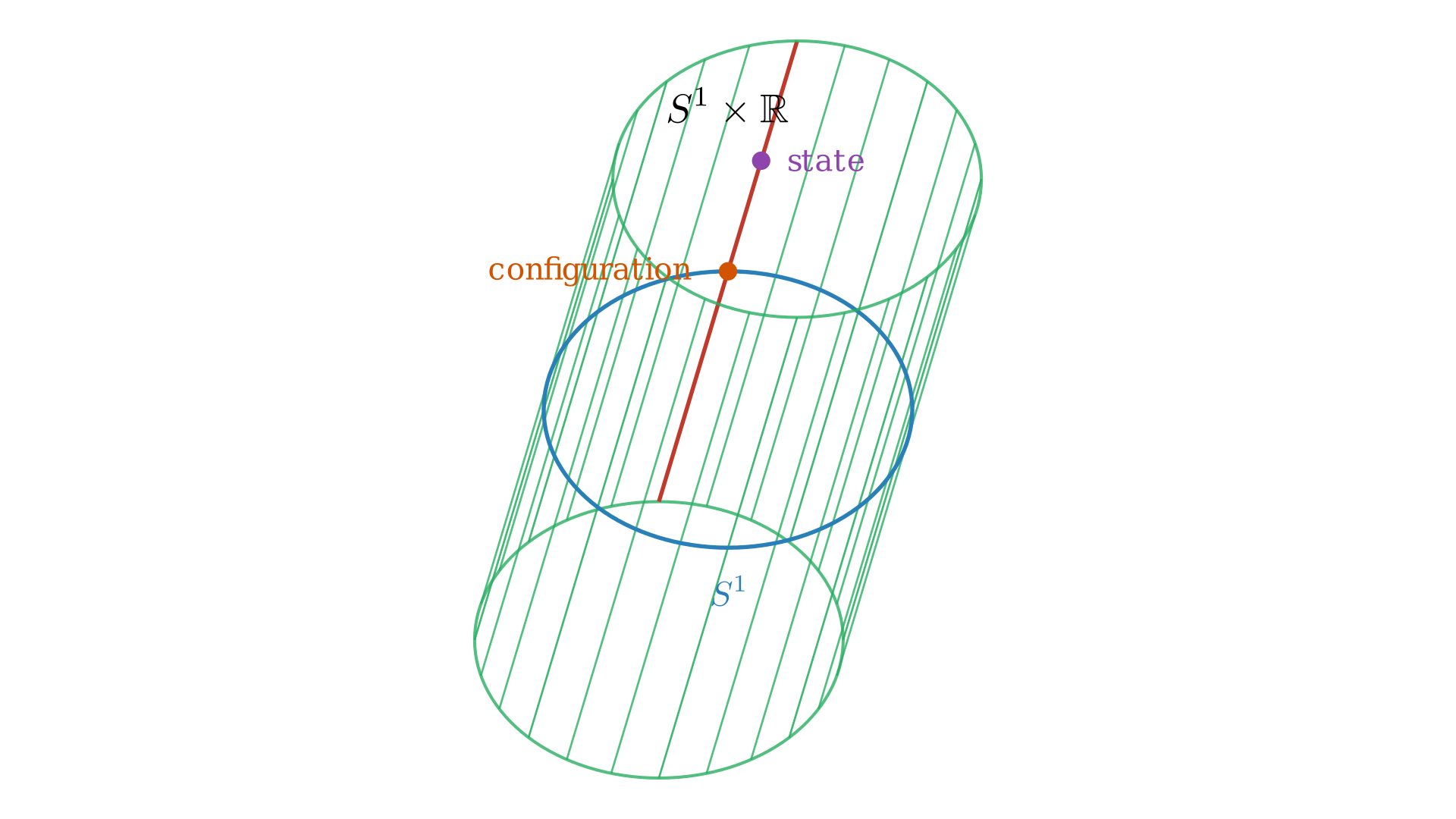
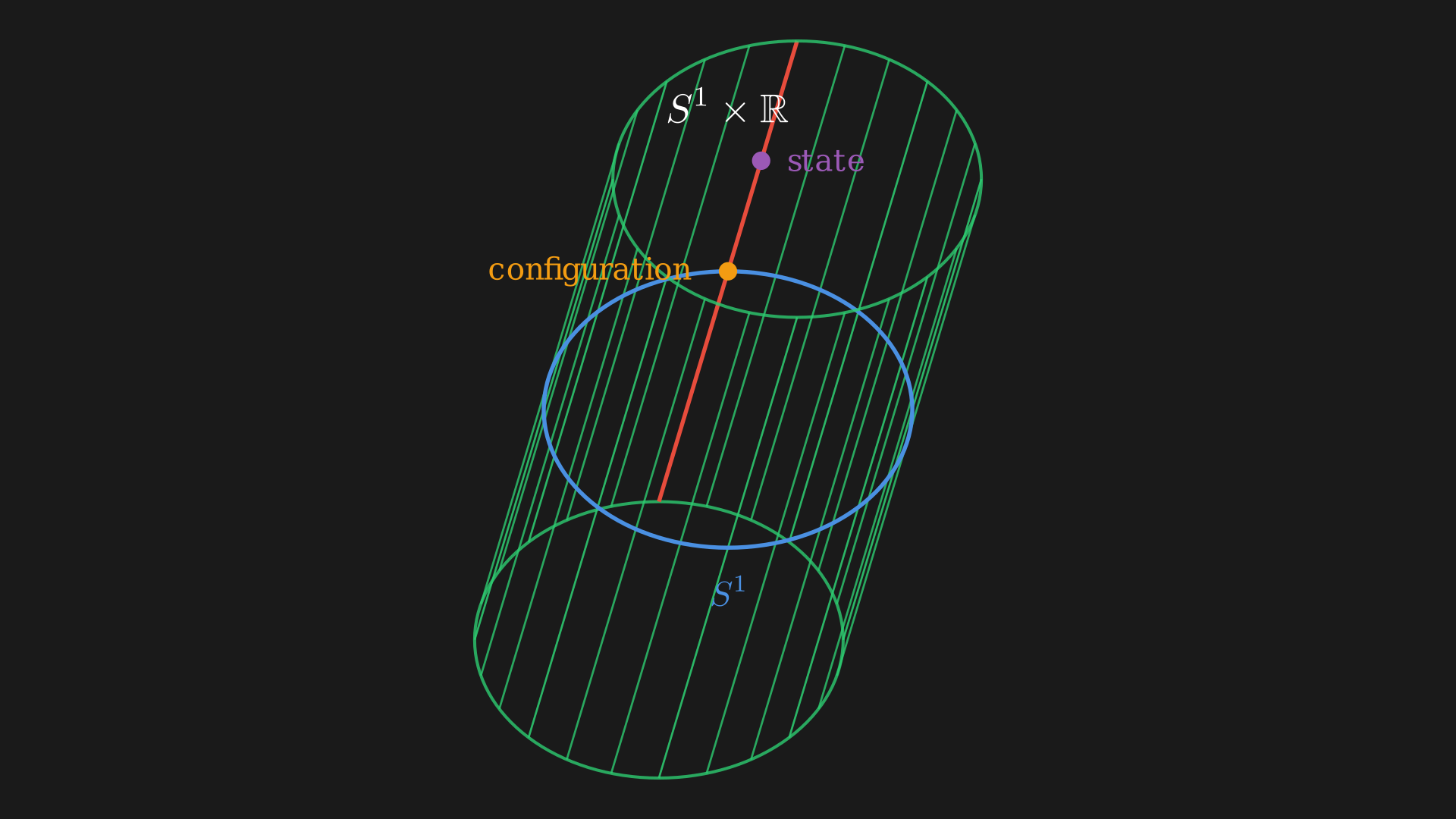
Every point on this cylinder is a state, and to analyze this state we can apply the projection map ¹ $\pi: T^*X \mapsto X, \pi: (q, p) \mapsto q$ which would map it down to the base space $S^1$ which is in the configuration space. At this point we have a cotangent fiber which is a $1$-dimensional vector space with the origin at the circle or the “zero momentum”. As we go up has a non-zero momentum. Every possible configuration and every possible velocity is represented in this cotangent bundle.

What this means is to specify the model of this state space all we need to do is provide a vector field on the space of states $T^*X$, that is have a tanegent vector throughout the cylinder. Thus, given any intiial state we can write the differenial equation for how we want to evolve the state according to the vector field or flow the vector field. The “equation of motion” is the equation for a flow-line of vector field which uniquely determines the “dyanmics” ².

The state space or phase space $M=T^*X$ has a has a natural geometric structure $w \in \Omega^2(M)$ which is called the symplectic form. This determines a Poisson bracket, $\lbrace ,\rbrace : C^\infty(M) \times C^\infty(M) \mapsto C^\infty(M)$³. This provides us a mechanism that allows us to get a map,

\begin{equation} \underbrace{C^\infty(M)}_{\text{functions on phase space}} \mapsto \overbrace{\Psi(M)}^{\text{vector fields on phase space}}, \end{equation} \begin{equation} f \mapsto X_f. \end{equation}

Essentially a function is converted to a vector field. This is very similar to gradient descent where we take the gradient of a function and move in the direction of the negative gradient. The gradient of the function $\nabla f$ gives you a vector field so it converts a function to a vector field too.

This is used to provide the vector field determining time evolution,

\begin{equation} \underbrace{H}_{\text{Hamiltonian function or energy}} \mapsto \overbrace{X_H}^{\text{time evolution}}. \end{equation}

So, the mathematical model underlying Hamiltonian mechanics is any system can be defined by only two things, (1) the configuration space and (2) the hamiltonian function to define the dynamics, \begin{equation} (\underbrace{X}_{\text{smooth manifold}}, \overbrace{H}^{\in C^{\infty}(T^*X)}). \end{equation}

Geometry of the Phase Space

The phase space $M=T^*X$ has a canonical $1$-form $\Theta \in \Omega^1(M)$ which means given any tangent vector to any point on the phase space we can evaluate (or give us a number) the $1$-form $\Theta$ at that point. So given a vector $u \in T_{(q, p)}M$ we can evaluate it,

\begin{equation} \Theta(u) = \overbrace{p}^{\text{covector at }q}(\underbrace{\pi_*u}_{\text{vector at }q}), \end{equation}

where $\pi_*$ is the derivative of the projection map $\pi$. The derivate of $\pi$ allows us to project the vector $u$ to to the $X$ or “downstairs”.

In co-ordinates, we have $u = \sum_{i=1}^n u^i \frac{\partial}{\partial q^i} + \sum_{i=1}^n p_i \frac{\partial}{\partial p_i}$ and $p = \sum_{i=1}^n p_i dq^i$ (a point in the cotangent space over $q$). This is the same as Equations \ref{eq:tangent-vector} and \ref{eq:cotangent-vector}, we write it in terms of basis and parameters. So,

\begin{equation} \begin{split} \Theta(u) &= p_i dq^i (u^j\frac{\partial}{\partial q^j} + u_j\frac{\partial}{\partial p_j}) \\
&= p_i u^i \\
&= p_idq^i \end{split} \label{eq:canonical-1-form} \end{equation}

If we write $\Theta$ or in general any $1$-form can written in basis, $\Theta = a_i dq^i + b^j dp_j$. When we evaluate $\Theta$ on $u$, the $a_i$ terms would combine with the $u^i$ terms and the $b_j$ terms would combine with the $u_i$ terms which would given us Equation \ref{eq:canonical-1-form} (the canonical $1$-form on $T^*X$). Essentially, $a_i$ becomes $p_i$ and $b^j$ becomes $0$.

Now, since the canonical $1$-form $\Theta \in \Omega^1(M)$ is differentiable we can obtain the $2$-form,

\begin{equation} \begin{split} \omega &= d\Theta \\
&= d(p_i dq^i) \\
&= dp_i \wedge dq^i \\
&= \underbrace{dp_1 \wedge dq^1 + dp_2 \wedge dq^2 + \cdots + dp_n \wedge dq^n}_{\text{symplectic form on }M}. \end{split} \label{eq:symplectic-form} \end{equation}

This is independent of the original choice of co-ordinates $q^i$. So if we do a co-ordinate changes $\tilde{q}^i = \tilde{q}^i(q^1, \ldots, q^n)$ this would give us new $\tilde{p}_i$ which is canonically conjugate to $\tilde{q}^i$, the $\omega$ would still be the same just in co-ordinates $(\tilde{q}^i, \tilde{p}_i)$ for the same $M$.

Interestingly, we can view the symplectic form $\omega$ as a skew-symmetric bilinear form on $T_{(q, p)}M$, $u_1, u_2 \in T_{(q, p)}M$ and $\omega(u_1, u_2) = -\omega(u_2, u_1)$ has matrix in basis $\frac{\partial}{\partial q}, \frac{\partial}{\partial p}$ as,

Essentially, we have,

\begin{equation} \underbrace{dp_i \wedge dq^i}_{\text{skew symmetric bilinear form}} \; \overbrace{(\cdot,\, \cdot)}^{\text{can plug in any two vectors}} \label{eq:skew-symmetric-bilinear-form} \end{equation}

The skew symmetric bilinear form in basis $\frac{\partial}{\partial q}, \frac{\partial}{\partial p}$.

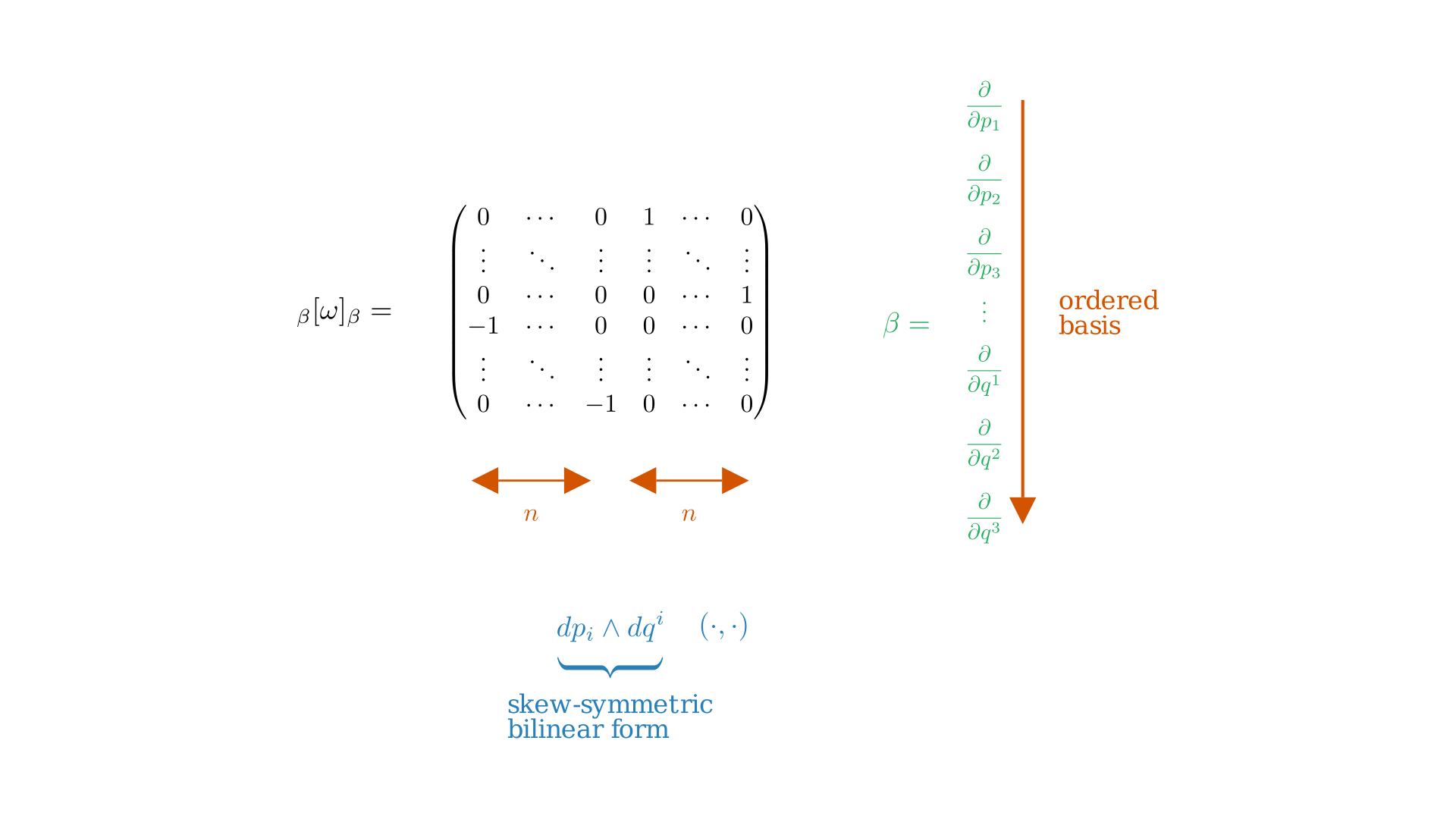
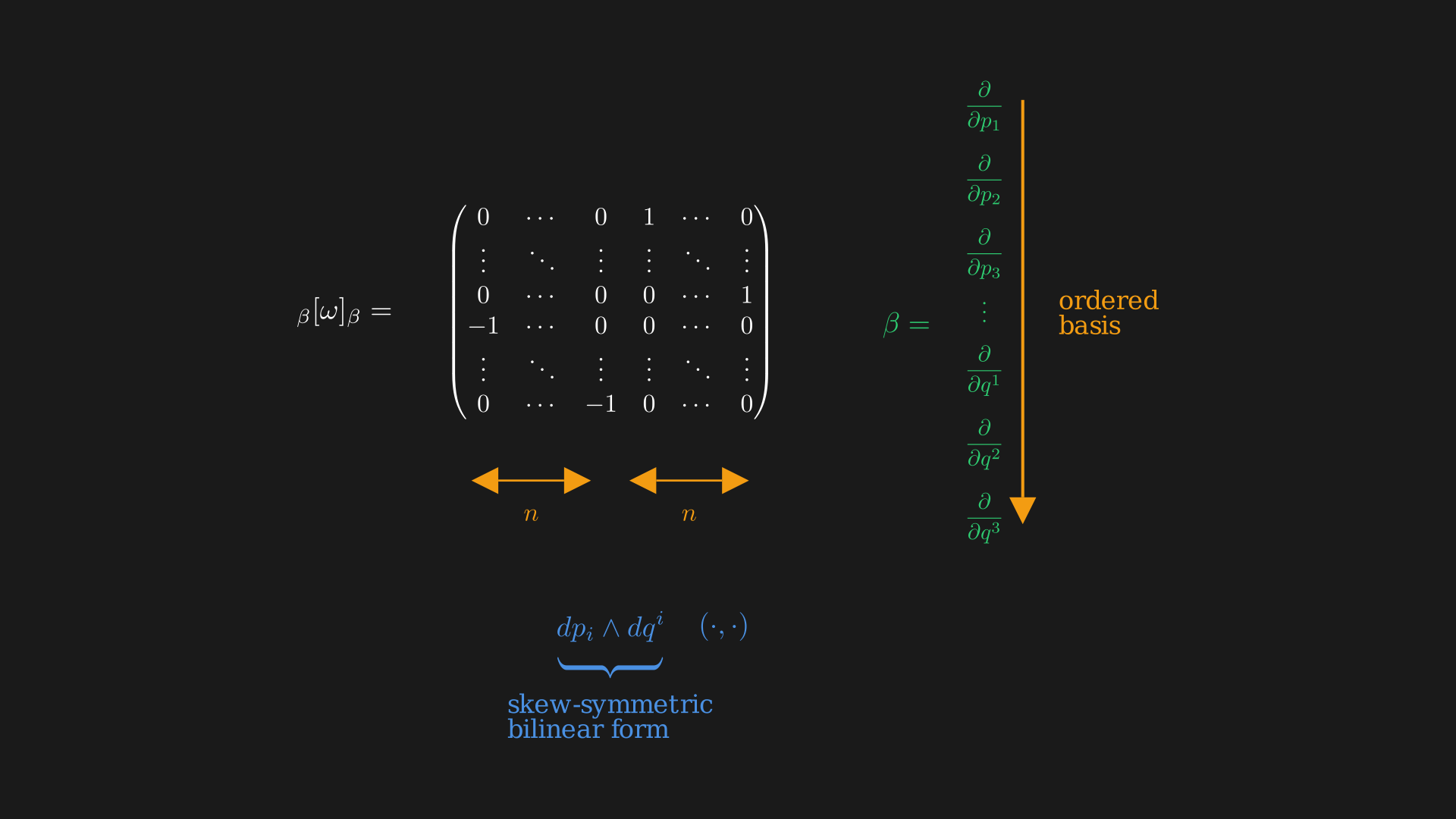
If we plug in the basis vectors $\frac{\partial}{\partial q^i}$ and $\frac{\partial}{\partial p_i}$ in Equation \eqref{eq:skew-symmetric-bilinear-form} we get the matrix. It is easy to see most of the entries are $0$ because we might get non-zero only when the momentum we plug in and the position we put in have the same index.

This gives us some properties of $\omega$,

1. $\omega$ is skew-symmetric, i.e. $\omega(u, v) = -\omega(v, u)$.
2. $\omega$ is closed, i.e. $d\omega = 0$ (notice that $\omega$ is $d(1$-form$)$).
3. $\omega$ is non-degenerate, i.e. $\omega(u, v) = 0$ for all $v \in T_{(q, p)}M$ implies $u = 0$.

This means, we can use it to define a map that takes a tangent vector to a vector on the phase space, $\omega: TM \mapsto T^*M$ or $\omega: u \mapsto \underbrace{\iota_u \omega}_{\text{interior product}} = \omega(u, \cdot)$. The $\cdot$ is a covector on the phase space. Since $\omega$ is non degenerate, this map is an isomorphism.

\begin{equation} \begin{split} \omega:& TM \mapsto T^*M \\
\omega:& u \mapsto \underbrace{\iota_u \omega}_{\text{interior product}} = \omega(u, \cdot) \\
\omega:& \frac{\partial}{\partial p_i} \mapsto \iota{\frac{\partial}{\partial p_i}} (dp_j \wedge dq^j) = \left( \iota{\frac{\partial}{\partial p_i}} dp_j \right) dq^j + (-1) dp_j \wedge \underbrace{(\iota{\frac{\partial}{\partial p_i}} dq^j)}_0 = dq^i \\
\omega:& \frac{\partial}{\partial q^i} \mapsto -dp_i. \\\ \end{split} \label{eq:omega-map} \end{equation}

So the momentum vector gets sent to the derivative of the position vector. and position vector gets sent to the negative derivative of the momentum vector. We essentially get to convert a tangent vector on phase space to a cotanget vector on phase space.

Hamiltonian Vector Field of $f$. This essentially gives us a way to convert $f \in C^\infty(M, \mathbb{R})$ to a vector field $X_f \in \Psi(M)$, \begin{equation} f \mapsto \underbrace{df}_{\in \Omega^1(M)} \mapsto -\omega^{-1}(df) = \underbrace{X_f}, \end{equation} where $X_f \in \Psi(M)$ is the Hamiltonian vector field associated to $f$.

The Hamiltonian vector field $X_f$ is such that,

1. Hamiltonian vector field of $f$ preserves itself. $X_f (f) = df (X_f) = df(-\omega^{-1}(df)) = -\omega^{-1}(df, df) = 0$ since $\omega$ is skew. However, this is very different from the gradient of $f$, on a Riemannian manifold $\nabla f = g^{-1}(df)$, $(\nabla f) (f) = df (g^{-1}df) = g^{-1}(df, df) = \mid \mid df \mid \mid^2$. Essentially, if the derivative is non-zero the gradient is not going to preserve the function. The hamiltonian vector field on the other hand preserves the level sets of $f$ or $f$ is conserved by the flow of $X_f$. And this is exactly why things like energy and momentum can be conserved, due to this feature of the Hamiltonian vector field.

2. Differentiating Symplectic form. in the direction of the vector field

\begin{equation} \begin{split} L_{X_f} \omega &= (d \iota_{X_f} + \iota_{X_f}d)\omega \\
&= d \iota_{X_f} \omega \\
&= d(\omega (-\omega^{-1}df, \cdot)) \\
&= d (-df) \\
&= 0, \end{split} \end{equation}

or $\omega$ is preserved, and where $\mathcal{L}$ is the Lie derivative. The hamiltonian vector field of a function $f$ is a symmetry of $(M, \omega , f)$. So, a hamiltonian systems consists of:

• a manifold $M$ (cotangent bandle of another manifold $X$)
• $\omega$ symplectic form on $M$ nondegenerate closed $2$-form ⁴
• a function $H$ or $f$, the hamiltonian

The Poisson bracket associated to $\omega$ is,

\begin{equation} \lbrace , \rbrace : C^\infty(M, \mathbb{R}) \times C^\infty(M, \mathbb{R}) \mapsto C^\infty(M, \mathbb{R}), \label{eq:poisson-bracket} \end{equation}

so we can take two functions $f$ and $g$ and one of these two functions determines a hamiltonian vector field and we can use this vector field to differentiate the other function,

\begin{equation} \lbrace f, g\rbrace = \color{red}{X_g(f)} = df (-\omega^{-1}(dg)) = \omega^{-1}(df, dg) = -\omega^{-1}(dg, df) = \color{red}{-X_f(g)}. \end{equation}

The Poisson bracket, Equation \eqref{eq:poisson-bracket} satisfies the Leibniz rule,

\begin{equation} \begin{split} \underbrace{\lbrace f_1f_2, g\rbrace }_{\text{differentiate product with vector field from $g$}} &= X_g(f_1f_2) \\
&= X_g(f_1)f_2 + f_1X_g(f_2) \\
&= \lbrace f_1, g\rbrace f_2 + f_1\lbrace f_2, g\rbrace \end{split} \end{equation}

(Poisson Algebra.) A Poisson algebra is a commutative algebra $A$ together with a bracket $\lbrace ,\rbrace : A \times A \mapsto A$ that is,

1. skew
2. satisfies the Leibniz rule $\lbrace f, gh\rbrace = \lbrace f, g\rbrace h + g\lbrace f, h\rbrace $
3. satisfies the Jacobi identity $\lbrace \lbrace f, g\rbrace , h\rbrace = \lbrace f, \lbrace g, h\rbrace \rbrace + \lbrace g, \lbrace f, h\rbrace \rbrace $.

Proof for Poisson Bracket satisfies the condition 3. Let $f, g, h \in C^\infty(M, \mathbb{R})$. Consider the $1$-parameter family of canonical transformations $\Phi_t$ generated by $h$, i.e. the flow of the Hamiltonian vector field $X_h$. For any observable $F$ set $F_t := F \circ \Phi_t$ and define the infinitesimal variation $\delta F := \left.\frac{d}{dt}\right\rvert_{t=0} F_t$. By our definition of the Poisson bracket and the fact that $X_h$ preserves $\omega$ (we already showed $\mathcal{L}_{X_h}\omega = 0$), we have \begin{equation} \delta F = X_h(F) = \lbrace F, h\rbrace. \label{eq:infinitesimal-variation} \end{equation} On the one hand, because $\Phi_t$ is a symplectomorphism it preserves the Poisson bracket, so \begin{equation} \delta\, \lbrace f, g\rbrace = X_h(\lbrace f, g\rbrace) = \lbrace \lbrace f, g\rbrace, h\rbrace. \label{eq:jacobi-hand-1} \end{equation} On the other hand, the change in $\lbrace f, g\rbrace$ comes only from the changes in $f$ and $g$ themselves. Using bilinearity and $\delta f = X_h(f) = \lbrace f, h\rbrace$ and $\delta g = X_h(g) = \lbrace g, h\rbrace$, we get \begin{equation} \begin{split} \delta\, \lbrace f, g\rbrace &= \lbrace \delta f, g\rbrace + \lbrace f, \delta g\rbrace \\\\ &= \lbrace \lbrace f, h\rbrace, g\rbrace + \lbrace f, \lbrace g, h\rbrace \rbrace. \end{split} \label{eq:jacobi-hand-2} \end{equation} Comparing \eqref{eq:jacobi-hand-1} and \eqref{eq:jacobi-hand-2} yields \begin{equation} \lbrace \lbrace f, g\rbrace, h\rbrace = \lbrace \lbrace f, h\rbrace, g\rbrace + \lbrace f, \lbrace g, h\rbrace \rbrace, \end{equation} which is equivalently the cyclic form \begin{equation} \lbrace \lbrace f, g\rbrace, h\rbrace + \lbrace \lbrace h, f\rbrace, g\rbrace + \lbrace \lbrace g, h\rbrace, f\rbrace = 0, \label{eq:jacobi-identity} \end{equation} exactly the Jacobi identity (condition 3).

The Poisson bracket is helpful for definiing the Hamiltonian flow, we know $C^\infty(M, \mathbb{R}) \ni H \mapsto X_H$ generates a flow, $\Phi_t^{X_H}: (\mathbb{R}, t) \times M \mapsto M$ such that $(t, m) \mapsto \Phi_t^{X_H}(m) = m(t)$ where $\frac{d}{dt}m(t) = X_H(m(t))$.

The Hamiltonian flow as a diffeomorphism on the phase space.

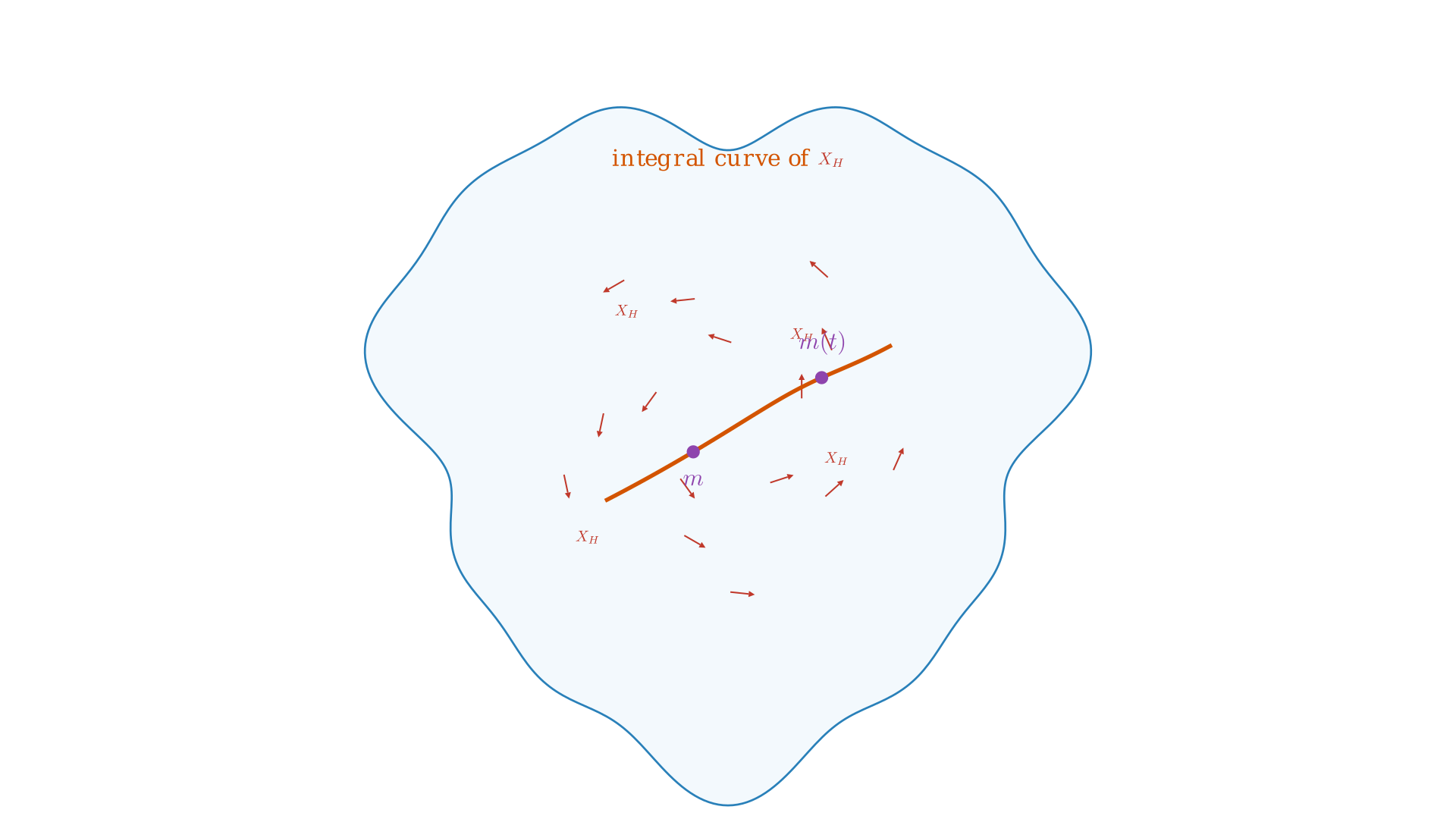
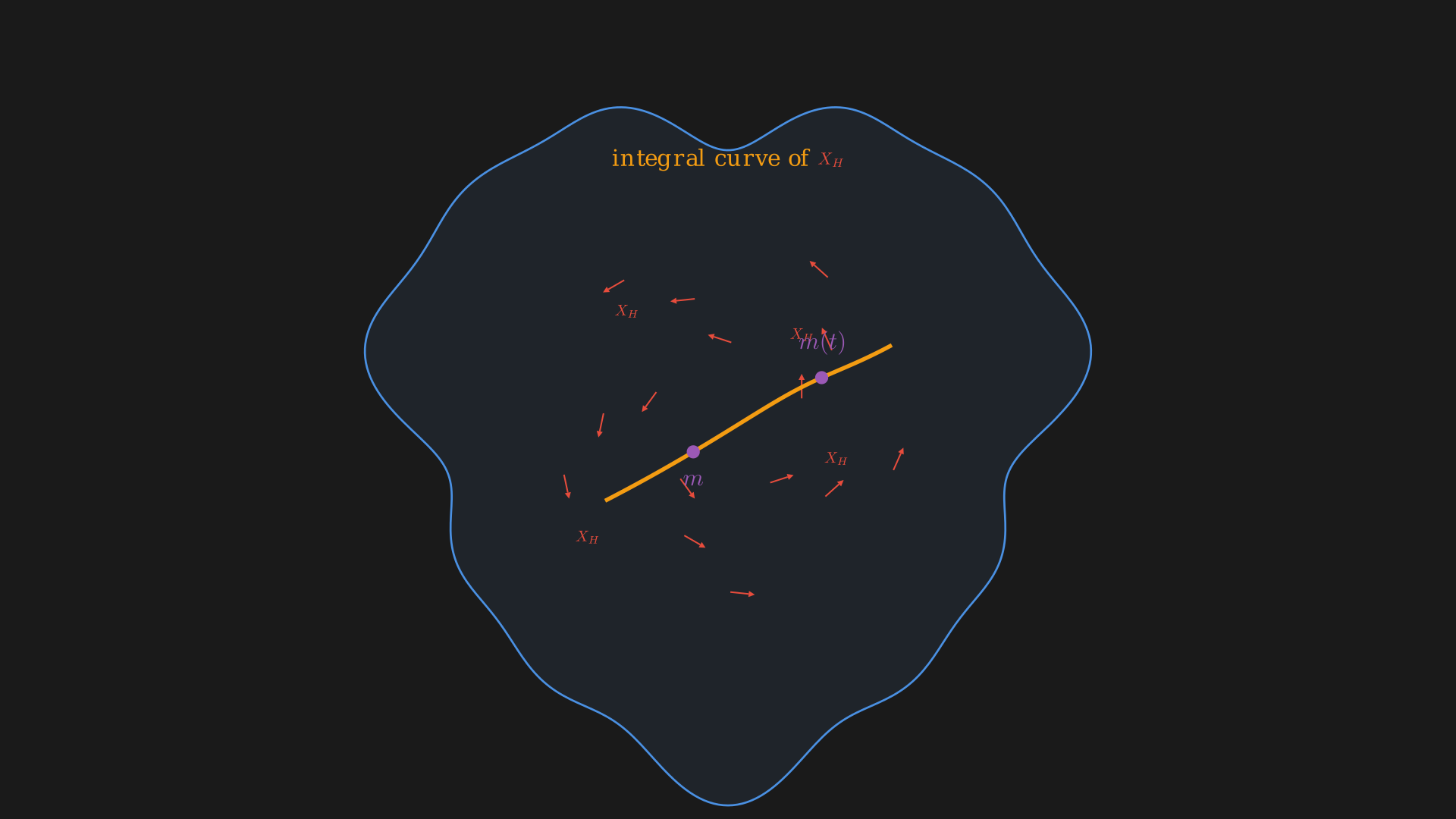
Alternatively, we can flow a function too, $f \in C^\infty(M, \mathbb{R})$ i.e. $f(t) = (\psi_t^{X_H})^*f$ since the flow is anwyas a diffeomorphism. What we essentially want is produce a path of functions such that at every moment in time the change in the function is given by the derivative along the vector field $\frac{d}{dt}f(t) = X_H(f(t)) = \underbrace{\lbrace f, H\rbrace}_{\text{Poisson bracket}}$ (Hamilton’s Equation). Essentially, the equation of motion for a function $f$ dragged along hamilton flow is the Poisson bracket.

In any Poisson algebra $(A, \lbrace ,\rbrace)$ we can write a similar equation. Fix $H \in \mathcal{A}$ then we can write a differential equation for a path $f(t)$ of elements in A: $\dot{f} = \lbrace f, H\rbrace$. We can think of the Hamiltonian flow as of every state, so if we choose a state we can see how it evolves in time or also describe a function and see how it evolves in time.

What this means is:

1. if we know initial state exactly we can find evolution $\dot{m}(t) = X_H(m(t))$
2. but if we only have probablistic information about the state say a density $\rho$, we can still get $\dot{\rho} = \lbrace \rho, H\rbrace$

Organizing Hamiltonians

Hamiltonians or functions on $M=T^*Q$ with some co-ordinates $(q^i, p_j)$. It does not make sense to classify functions based on the degree of $q$ because that is dependent on the choice of co-ordinate system we have. But we can organize hamiltonians based on degree in vector space directions $p_i$.

Degree 0

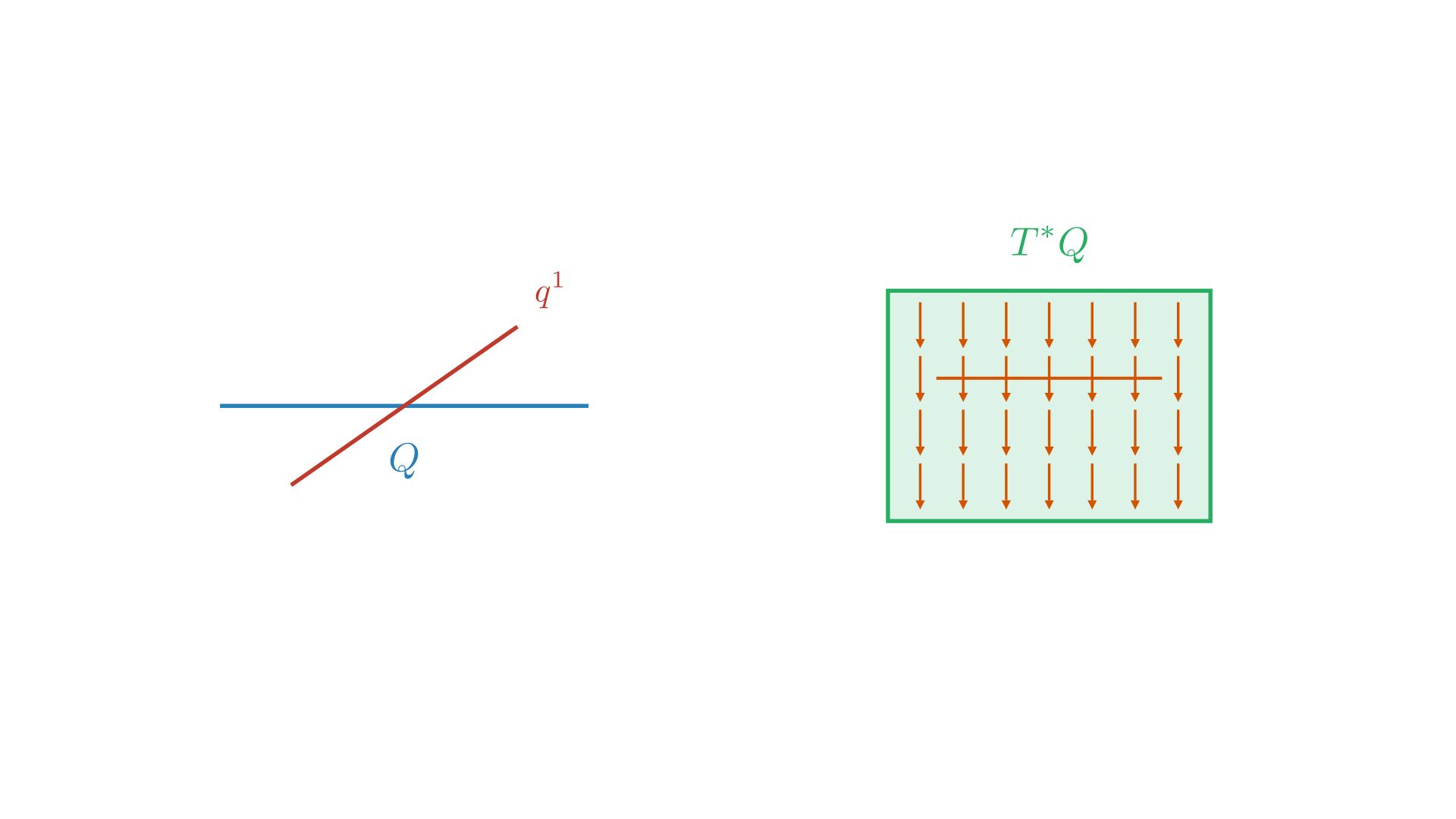
First, we have functions which are constant in cotangent directions so the functions is over $q$ not of $p$, $f=V(q^1, \ldots, q^n)$. This is like saying $f$ is pulled back from $V \in C^{\infty}(Q, \mathbb{R})$. So, $M=T^*Q \rightarrow ^{(\pi)} Q \rightarrow ^{(V)} \mathbb{R}$ or $\pi^*V = V \circ \pi: M \to \mathbb{R}$.

If we take $V=q^1$, then $X_v = -\omega^{-1}dV = -\omega^{-1}dq^1 = -\frac{\partial}{\partial p_1}$ (from Equation \eqref{eq:omega-map}). As we expect, the level sets of Hamiltonians are preserved by the Hamiltonian flow. The effect this has is we stay at the same position but our momentum is increased.

The Hamiltonian flow of a degree 0 Hamiltonian.

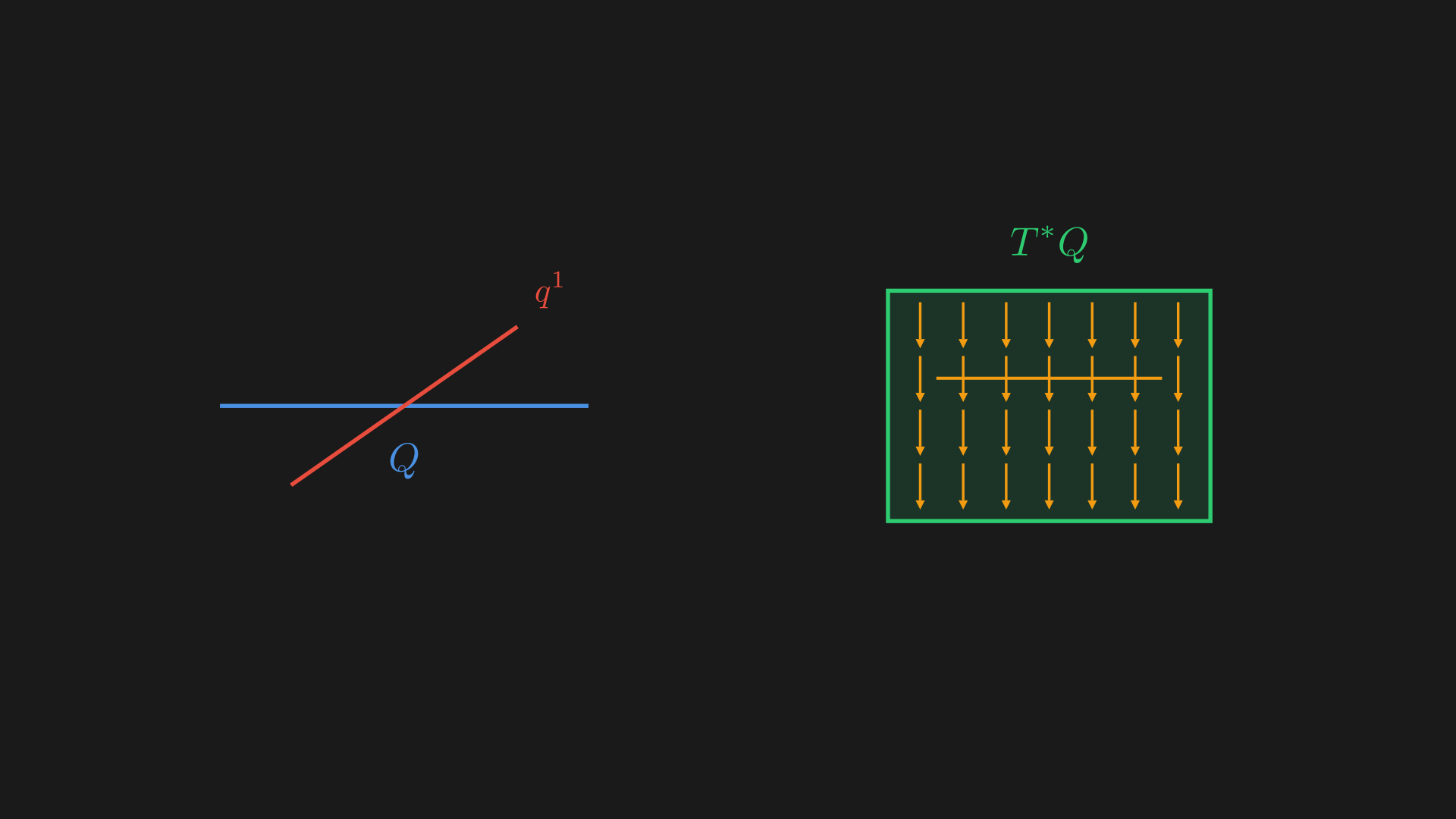
Degree 1

$f = V^1 p_1 + V^2 p_2 + \cdots + V^n p_n$, this is a linear combinations of $p$, the coefficient $V^i$ is any smooth function of $q$, $V^i = V^i(q^1, \ldots, q^n)$. So now, the hamiltonian vector field of this function is,

\[\begin{equation} \begin{split} X_f &= -\omega^{-1}(df) \\ &= -\omega^{-1}(p_i dV^i + V^i dp_i) \\ &= -\omega^{-1}(p_i \frac{\partial V^i}{\partial q^j} + V^i dp_i) \\ &= -p_i \frac{\partial V^i}{\partial q^j}\frac{\partial}{\partial p_j} + V^i \frac{\partial}{\partial q^i} \\ \end{split} \end{equation} \label{eq:hamiltonian-vector-field-degree-1}\]

We now have a term that has a vertical component $\frac{\partial}{\partial p_j}$ for the Hamiltonian flow depending on the magnitude of the momentum. This guarantees that the Hamiltonian flow has, $\frac{d}{dt}q^i = V^i(q^1, \ldots, q^n)$ because there is only one term changing $q^i$, $V^i \frac{\partial}{\partial q^i}$. We can use the ODE $\frac{d}{dt}q^i = V^i(q^1, \ldots, q^n)$ to directly get the positions in this case.

We can also see how the $p_j$ is changing, $\frac{d}{dt}p_j = -p_i\frac{\partial V^i}{\partial x^j}$. The phase portrait would look like something where the $x$-axis is given by the ODE for $q^i$ and the $y$-axis is given by the ODE for $p_j$.

For example, consider $f=p_1$ which is set $V^1=1$, $V^2=V^3=\cdots=0$. Then, $X_f = -\omega^{-1}(dp_1) = \frac{\partial}{\partial q^1}$ or we don’t have the first term at all in Equation \eqref{eq:hamiltonian-vector-field-degree-1}. This is is another way of saying the momentum function generates spatial translation or when we flow of hamiltonian vector field for time $t$,

\[\begin{equation} \Psi_t^{X_f}: (q, p) \mapsto (q + \underbrace{(t, 0, \ldots, 0)}_{\text{translate in $q^1$ direction}}, p) \end{equation}\]

We can think of this as for degree $0$ we have functions on $Q$, $C^\infty(Q)$ and for degree $1$ we have vector fields on $Q$, $\mathfrak{X}(Q) = \underbrace{\Gamma(Q, TQ)}_{\text{section of tangent bundle of }Q}$.

The Hamiltonian flow of a degree 1 Hamiltonian.

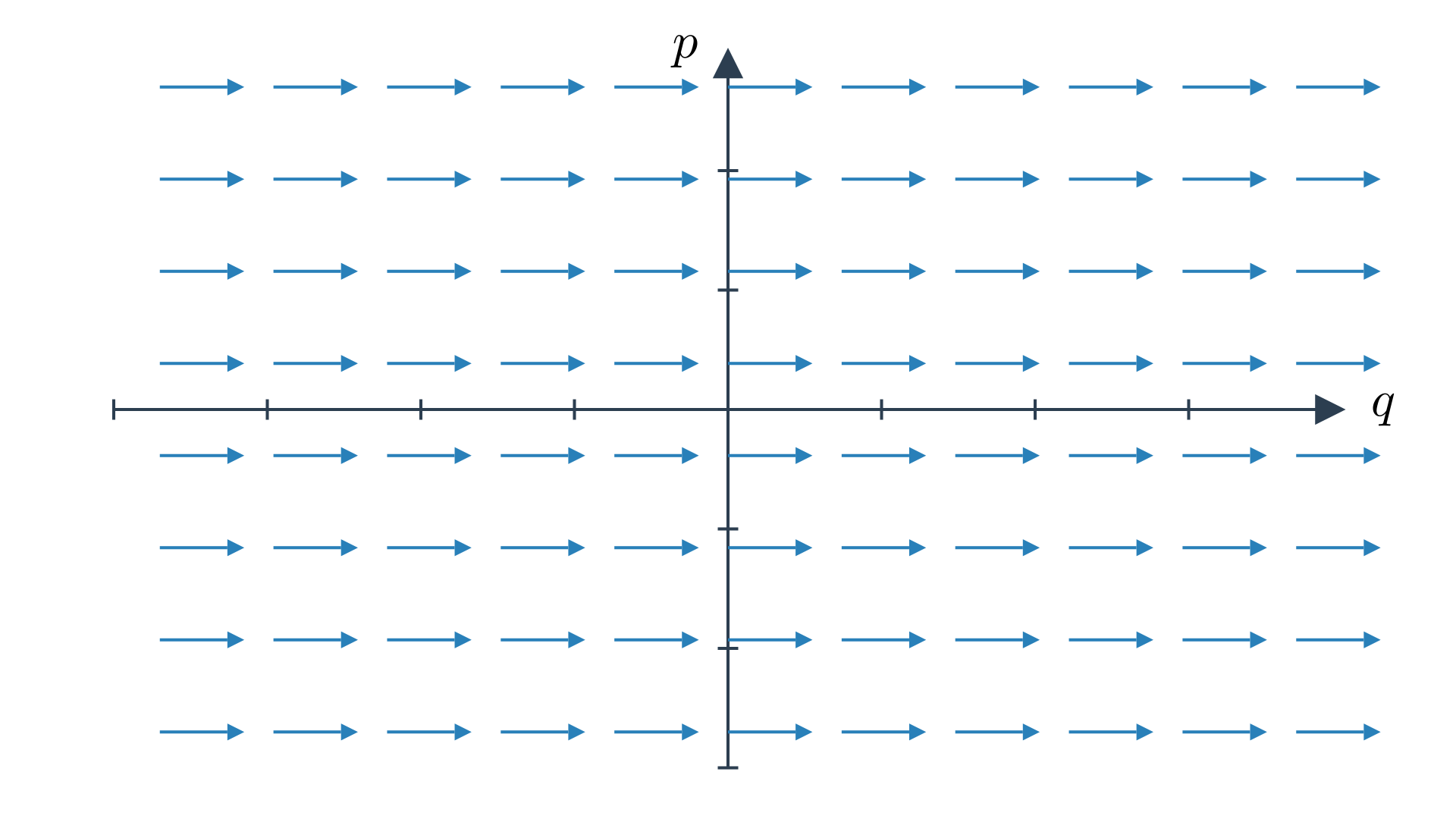
The function we have is linear in the direction of fiber so it is $0$ in the zero section of the cotangent bundle and grow linearly in the direction of the fiber. Because of this, they are elements of the dual space of the cotangent fiber and thus are tangent vectors. Since $f\in C^\infty(T^*Q)$ is linear on $T*Q$ fibres, it defines a tangent vector at every point in $Q$. Thus, Hamiltonians of degree 1 are $\mathfrak{X}(Q)$, vector fields on $Q$. Like, $f = V^1 p_1 + \ldots + V^n p_n$ corresponds to the vector field $V = V^i \frac{\partial}{\partial q^i}$.

(Proposition.) There is a vector field $V$ on $Q$ which generates a flow on $Q$, it induces a diffeomorphism on $Q$. This means it also induces a diffeomorphism on $T^\*Q$. This induced diffeomorphism or symmetry is the hamiltonian flow of the function determined by $V$.

Hamiltonian flow of $f_V = V^ip_i$ coincides with the flow on $T^\*Q$ induced by the flow of $V$ on $Q$.

Degree 2

Here, we have $f = V^{ij}p_ip_j$, $V^{ij} \in C^\infty(Q)$. To specify this function we need to specify the coefficients $V^{ij}$ so we need $\frac{1}{2}n(n+1)$ smooth functions of $q^1, \ldots, q^n$.

For example, let us suppose we are given a Riemannian metric $g$ on $Q$. We have a tensor $g = g_{ij}(q^1, \ldots, q^n)dq^i \otimes dq^j$ where the $g_{ij}$ term is a symmetric matrix of $n \times n$ smooth functions of $q^1, \ldots, q^n$, is non-degenerate at every point, and positive definite. Without talking about co-ordinates we can say $g$ defines a map $g: TQ \mapsto T^*Q$ which is an isomorphism. Any vector $v$ we put in $g$ gives us some covector $g(v, \cdot)$. We also have $g^{-1}: T^*Q \mapsto TQ$ which takes in two inner forms to compute an inner product of, $g^{-1} = g^{ij} \frac{\partial}{\partial q^i} \otimes \frac{\partial}{\partial q^j}$ where $g^{ij}$ is the inverse of $g_{ij}$. This defines a quadratic function $\frac{1}{2}f_{g^{-1}} = \frac{1}{2}g^{ij}(q^1, \ldots, q^n)p_ip_j$.

What this means is if you take $Q$ and have the tangent spaces at each point $T^*Q$. On $Q$ where $p=0$ the function is $0$ and on $T^*Q$ where $p \neq 0$ the function grows quadratically as we move on $T^*Q$ so we get ellipsoids or level sets of $fg^{-1}$. Connecting many of these level sets across different points of $Q$ we get cylindrical level sets of $fg^{-1}$ are called the cosphere bundles inside $T^*Q$.

The cosphere bundle.

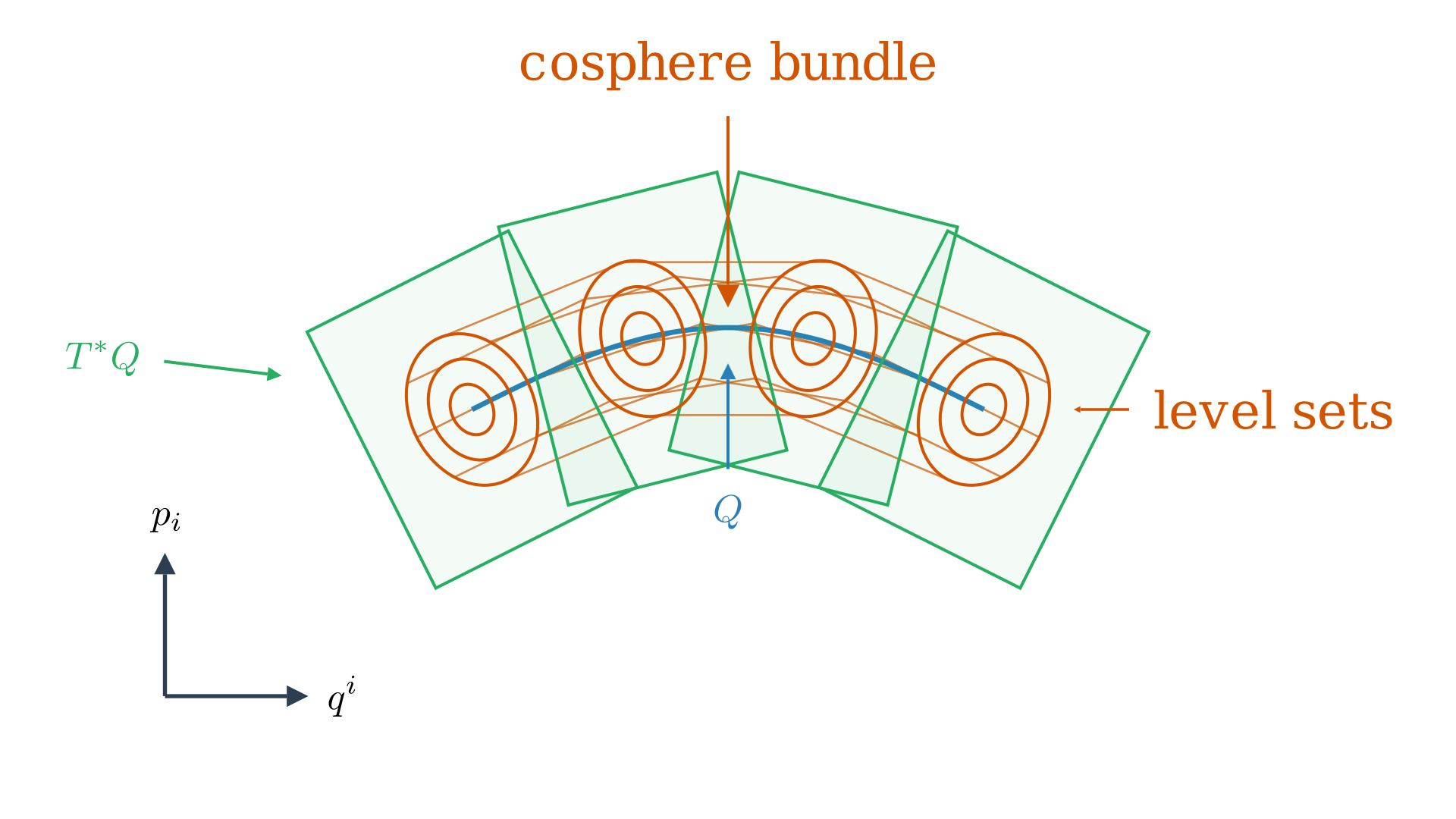
Now, we can think about the Hamiltonian flow of $f_{g^{-1}}$ defined by the Riemannian metric $g$. If you are inside the cosphere bundle on the hase space and as Hamiltonian flow progress we will stay inside the cosphere bundle, and the Riemannian metric or the norm-squared of the momentum is preserved. Interestingly, this function $\frac{1}{2}f_{g^{-1}}$ is the exact definition of kinetic energy of a particle on $Q$ (this definition works on any Riemannian manifold).

The Hamiltonian is,

\[\begin{equation} \begin{split} H &= \frac{1}{2}g^{ij}(q^1, \ldots, q^n)p_ip_j\\ dH&= \frac{1}{2} d(g^{ij}(q^1, \ldots, q^n)p_ip_j) p_i dp_j + \frac{1}{2} g^{ij}(q^1, \ldots, q^n)p_i dp_j\\ &= \frac{1}{2} \frac{\partial g^{ij}}{\partial q^k}p_ip_j dq^k + \frac{1}{2} g^{ij}(q^1, \ldots, q^n)p_i dp_j\\ -\omega^{-1}(dH)&= \frac{1}{2} \frac{\partial g^{ij}}{\partial q^k}p_ip_j dq^k\frac{\partial}{\partial p_k} + \frac{1}{2} g^{ij}(q^1, \ldots, q^n)p_i \frac{\partial}{\partial q^j} \end{split} \label{eq:hamiltonian-degree-2} \end{equation}\]

So, we have the ODEs

\[\begin{equation} \begin{split} \dot{q}^j &= g^{ij}p_i \\ \dot{p}_j &= -\frac{1}{2}\partial_k g^{ij}p_i p_j \end{split} \label{eq:hamiltonian-degree-2-ode} \end{equation}\]

One very interesting way of thinking about this is, compare the defintion of Kinetic Energy to $\frac{1}{2}mv^2$ then the Rimeannian metric $g$ is the analog of the mass. What the hamiltonian flow is growing with $p$ in the horixontal direction, which is like saying if our momentum is large we need to move faster at the same mass.

It turns out to get physically meaningful interprattion, we actually need to start with this degree $2$ Hamiltonian which makes the relation between the momentum and the velocity clear.

However, there is one thing we need to be careful of. Let us see Equation \eqref{eq:hamiltonian-degree-2}, it says for momentum ODE the derivative of it is related to square of the momentum. This is like the non-linear ODE Ricati equation $\dot{y} = y^2$. Teh Ricati equation goes to $\infty$ in a finite time. And this problem can exist in vector field too, the velocity can go to $\infty$ in a finite time of the flow. This eerily reminds me of Lagrangian mechanics where we use time integrators like Forward Euler which have exactly the same problem.

If the flow exists for all time, we say $(Q, g)$ is a complete Riemannian manifold. The solutions $(q(t), p(t))$ determine parameterized curves $q(t)$ in $Q$. These curves are geodesics on the original Riemannian manifold. The geodesic equation is actually hamiltonian! We can write the geodesic equation as,

\[\begin{equation} \gamma: \mathbb{R} \mapsto (Q, g) \end{equation}\]

where $\gamma$ is the parametric curve in $Q$. $\dot{\gamma} \in \Gamma(\mathbb{R}, \gamma^*TQ)$. The popular Levi-Civita connection is $\nabla_{\frac{\partial}{\partial t}} \dot{\gamma} = 0$ or acceleration is zero that is $\gamma(t) = (q^1(t), q^2(t), \ldots, q^n(t))$. The geodesic equation says,

\[\begin{equation} \ddot{q}^i + \Gamma^i_{jk} \dot{q}^j \dot{q}^k = 0 \label{eq:geodesic-equation} \end{equation}\]

where $\Gamma^i_{jk}$ is the Christoffel symbol $\Gamma^i_{jk} = \frac{1}{2} g^{im}(\frac{\partial g_{mj}}{\partial q^k} + \frac{\partial g_{mk}}{\partial q^j} - \frac{\partial g_{jk}}{\partial q^m})$. As it turns out, after some work the geodesic equation is exactly equivalent to the second degree ODEs in Equation \eqref{eq:hamiltonian-degree-2-ode}.

We can think of this as to analyze geodesic equations, all we can do is have the metric determine the function of the cotangent bundle and that function determine a flow. This flow is the geodesic flow.

What do we get from these degrees?

• Degree 0: Function on the configuration space $V \in C^\infty(X, \mathbb{R})$ (potential)
• Degree 1: Vector fields on the configuration space, $Y \in \mathfrak{X}$
• Degree 2: $T_g = \frac{1}{2} f_g^{-1}$ with a Riemannian metric $g$ (kinetic energy)

An example is taking the degree $0$ and the degree $2$ and putting them together,

\[\begin{equation} \begin{split} H &= T_g + V \\ \underbrace{X_H}_{\text{hamiltonian vector field}} &= \overbrace{X_g}^{\text{geodesic vector field}} + \underbrace{X_v}_{\text{deflection due to forces by potential field}} \end{split} \label{eq:hamiltonian-degree-0-and-2} \end{equation}\]

From Hamilton's equations of motions we know, $$ \begin{equation} \begin{split} \dot{q}^i &= \{q^i, H\} \\ \dot{p}_i &= \{p_i, H\} \end{split} \label{eq:hamiltonian-degree-0-and-2-ode} \end{equation} $$

For $X_g$ we have,

\[\begin{equation} \begin{split} X_g:&\qquad \dot{q} = g^{-1}p \\ &\qquad \dot{p}_i = \frac{1}{2}\partial_k g^{ij}p_i p_j \end{split} \end{equation}\]

For $X_v = -\omega^{-1}(dV) = (dp_i \wedge dq^i)^{-1}(\partial_k V dq^k)$ we have,

\[\begin{equation} \begin{split} X_v:&\qquad \dot{q} = 0 \\ &\qquad \dot{p} = -\frac{\partial V}{\partial q^i} \end{split} \end{equation}\]

Combining the Levi-Civita connection we get,

\[\begin{equation} \begin{split} &\nabla_{\frac{\partial}{\partial t}} \dot{q} = -\overbrace{g^{-1} (dV)}^{\operatorname{grad}(V)} = g^{-1}F \\ \implies & F = ga = g \nabla_{\frac{\partial}{\partial t}} \dot{q} \end{split} \end{equation}\]

This system takes in a force with using the potnetial $V$ and the Riemannian metric $g$ is the equivalent of the mass. I you look at this example it recovers all Newtonian systems.

An Oscillator

Let us consider a simple oscillator. At this stage, I highly recommend read my article on the simulation first where I talk about many of these kind of systems at length.

An example of a simple configuration.

Equip $X$ with Riemannian metric $g$ where $g = m dq \otimes dq$. Here the metric tensor is just the $1 \times 1$ identity matrix so $T_g=\frac{1}{2}mp^2$. We also need to provide a law of force for a spring, from Hooke’s law we have $V=\frac{1}{2}kq^2$.

The Hamiltonian for this system, or for $X= (\mathbb{R}, q)$ and $T^*X= (\mathbb{R} \times \mathbb{R}, (q,p))$ is,

\[\begin{equation} H = \frac{1}{2}m^{-1}p^2 + \frac{1}{2}kq^2 \end{equation}\]

The hamiltonian vector field is,

\[\begin{equation} X_H = m^{-1}p \frac{\partial}{\partial q} - kq \frac{\partial}{\partial p} \label{eq:hamiltonian-vector-field-oscillator} \end{equation}\]

The vector field would be a rotational vector field, something like the below image taken from my article on the simulation (you should read this to directly connect this view to the Lagrangian view). Essentially the vector field gets bigger as we move away from the origin.

The vector field for the oscillator.

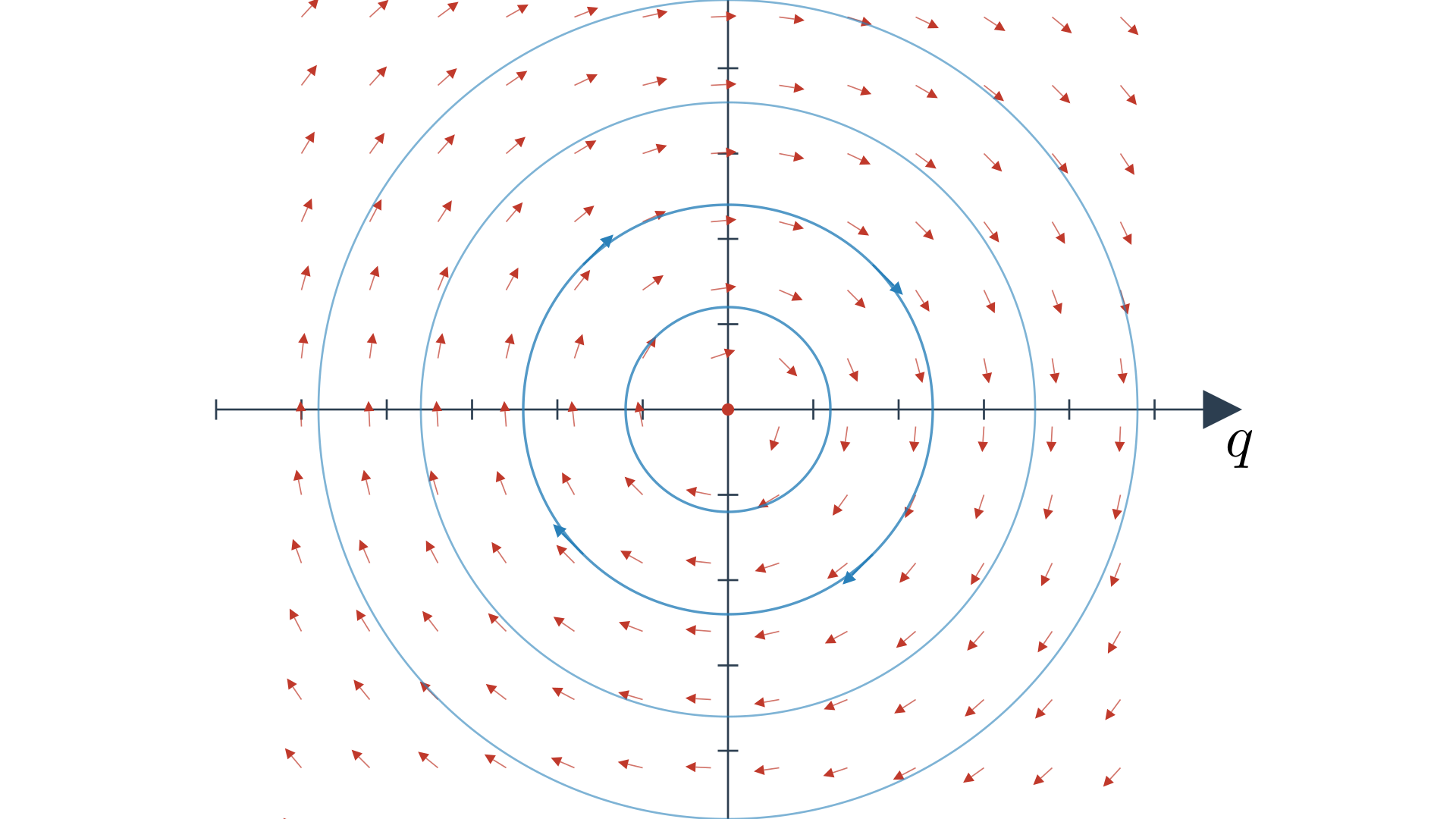
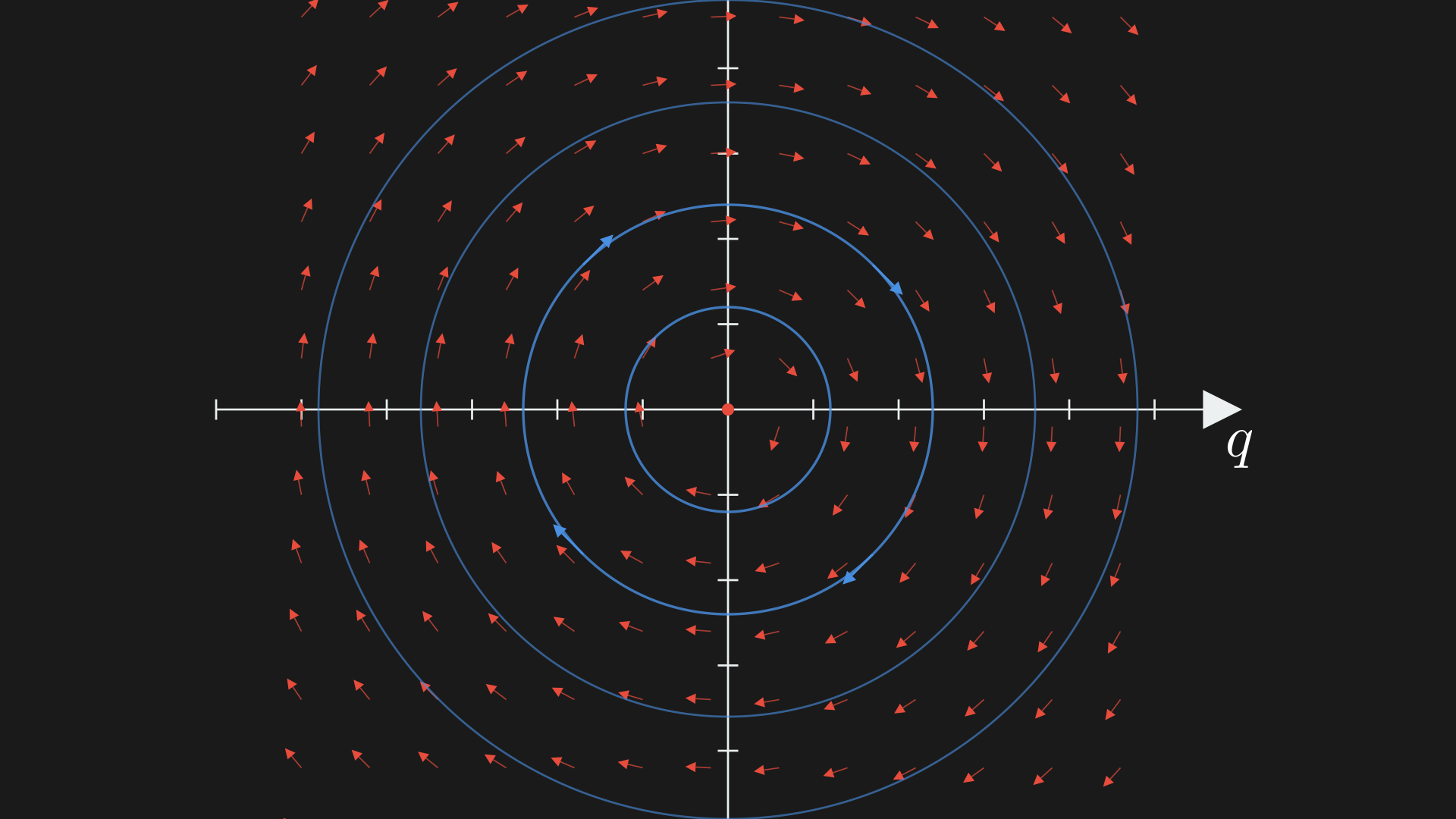
An interesting thing to note here is that the vector field (Equation \eqref{eq:hamiltonian-vector-field-oscillator}) is linear which makes it scale linearly as we scale the points in the cotangent bundle. In only this case, the cotangent bundle is a vector space. So, we can we can represent Hamilton’s equations in matrix form as,

\[\begin{equation} \frac{d}{dt} \begin{pmatrix} q \\ p \end{pmatrix} = \underbrace{\begin{pmatrix} 0 & m^{-1} \\ -k & 0 \end{pmatrix}}_{A} \begin{pmatrix} q \\ p \end{pmatrix} \end{equation}\]

The solution to this is,

\[\begin{equation} \begin{pmatrix} q(t) \\ p(t) \end{pmatrix} = e^{At} \begin{pmatrix} q(0) \\ p(0) \end{pmatrix} \label{eq:solution-oscillator} \end{equation}\]

Does this look familiar? It is exactly what we get from the Lagrangian view! What we can do similarly is notice $A^2 = -k m^{-1} \mathbb{I} = -\omega^2 \mathbb{I}$ so we can scale $A$ such that it squares to the negative of the identity matrix or the operator behavies like a complex number $(\underbrace{\omega^{-1} A}_J)^2=-\mathbb{I}$. So,

\[\begin{equation} (\omega^{-1} A) = J = \left(\sqrt{\frac{k}{m}}\right)^{-1} \begin{pmatrix} 0 & m^{-1} \\ -k & 0 \end{pmatrix} = \begin{pmatrix} 0 & \frac{1}{\sqrt{km}} \\ -\sqrt{km} & 0 \end{pmatrix} \end{equation}\]

So looking at the solution (Equation \eqref{eq:solution-oscillator}) we can write it using Euler’s formula ($e^{i\theta} = \cos(\theta) + i\sin(\theta)$),

\[\begin{equation} \begin{pmatrix} q(t) \\ p(t) \end{pmatrix} = e^{twJ} \begin{pmatrix} q(0) \\ p(0) \end{pmatrix} = \left(\cos(\omega t) \mathbb{I} + \sin(\omega t) J\right) \begin{pmatrix} q(0) \\ p(0) \end{pmatrix} \end{equation}\]

So, $q(t) = \cos(\omega t) q(0) + \underbrace{\frac{1}{\sqrt{km}} \sin(\omega t) p(0)}_{\omega^{-1}\sin{\omega t}\dot{x}(0)}$. An example is if you pull a mass and leave it, we wont have the second term because starting velocity is $0$ and we would oscillate with the cosine function in the first term, oscillation with frequency $\omega$.

Here we can simply change the variables or do a symplectomorphism to get rid some varibles, use $\tilde{q} = \sqrt{k}q$ and $\tilde{p} = \frac{1}{\sqrt{k}}$, so $H = \frac{1}{2}m^{-1}(k\tilde{p})^2 + \frac{1}{2}\tilde{q}^2$.

This system has a few pretty well known properties in $k=m=1$,

• all of its trajectories are closed curves in the phase space
• the periods are all given by $T=\frac{2\pi}{\omega}$

We get the period by doing one cycle $\int dt = T$ by fixing the energy $H^{-1}(E)$. If we use co-ordinate $x$ on curve $e$ then $T=\int_e \frac{dx}{{x,H}}$ and remember ${\cdot}$ is the Poisson bracket. We have, ${x,p} = \frac{\partial x}{\partial x}\frac{\partial p}{\partial p} - \frac{\partial x}{\partial p}\frac{\partial p}{\partial x} = 1$ and ${x,x} = 0$. Also, ${x, \frac{1}{2}(p^2+x^2)} = 2 \frac{1}{2}p {x,p} = p$. Further, given $\frac{1}{2} (x^2+p^2) = E$ we have $T = \int_e \frac{dx}{\sqrt{2E-x^2}}$.

Now split the circle curve into two.

The energy level circle and the two curves.

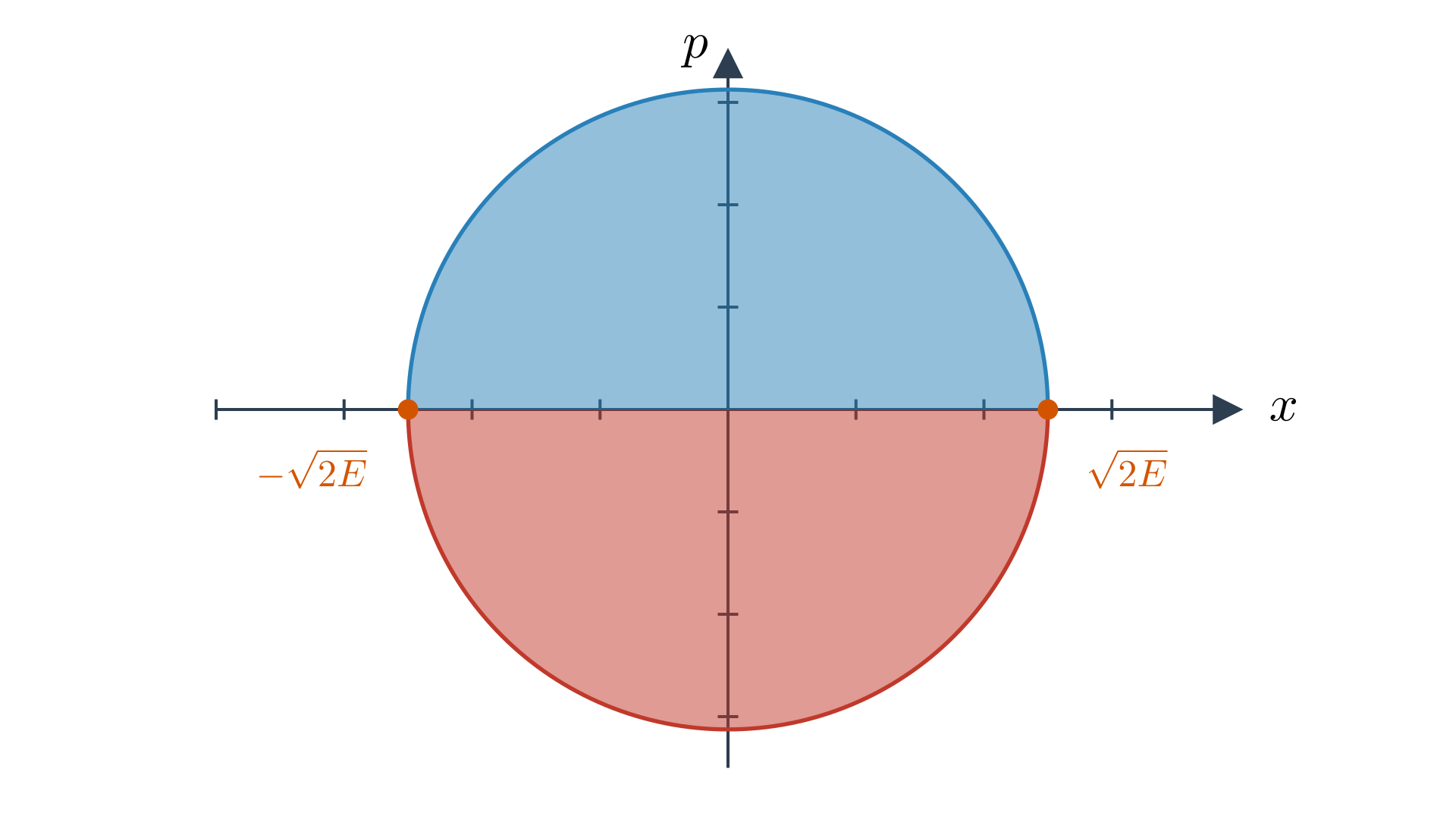
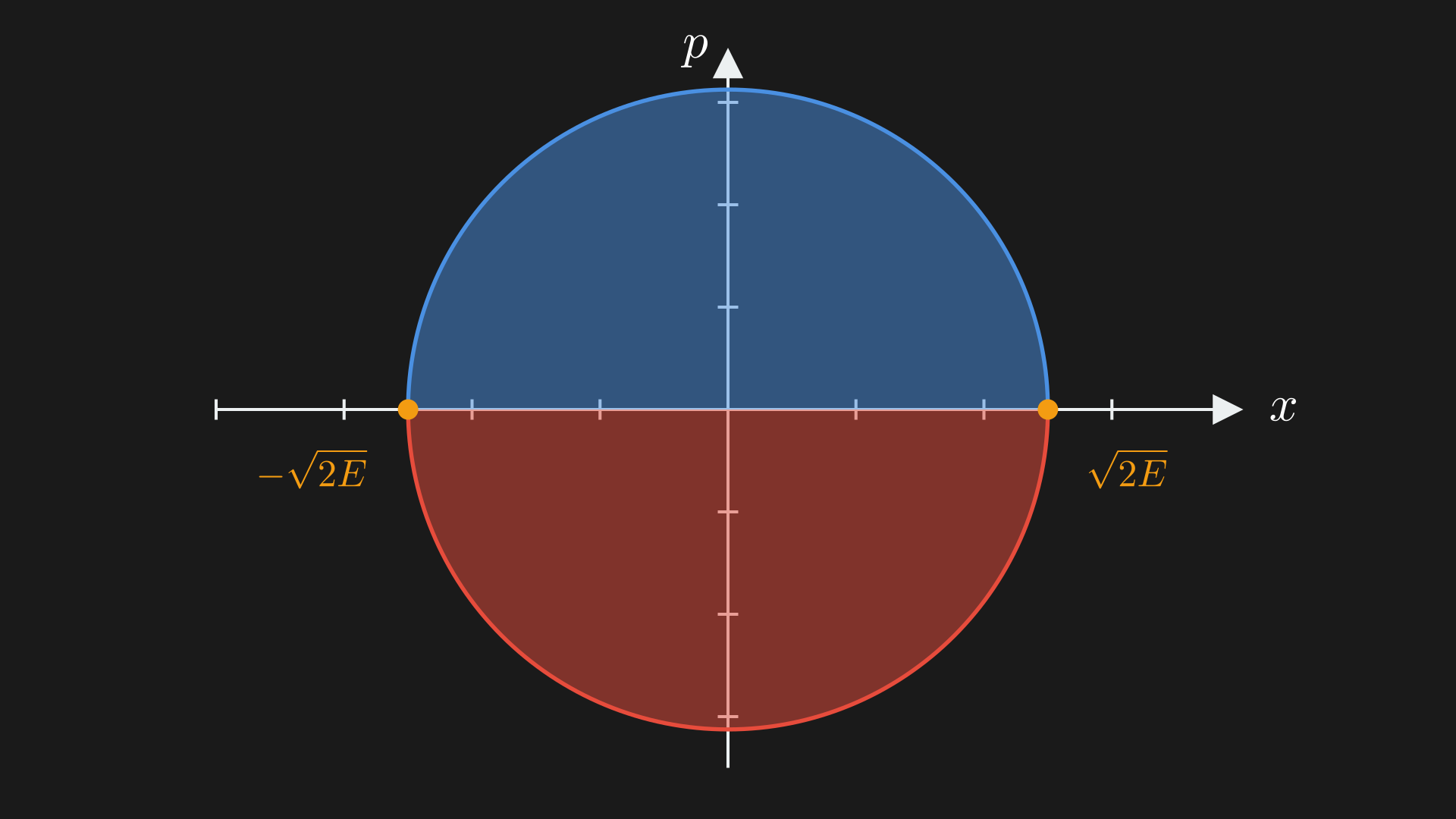
and we end up with $T = 2 \int_{-\sqrt{2E}}^{\sqrt{2E}} \frac{dx}{\sqrt{2E-x^2}} = 2\pi$. This is super interesting because we start out with algebraic data, this algebraic data determines a flow which determines integral which gives rise to a transcedental numbers from simple algebraic operations.

References and Footnotes

1. Why is there a projection? By how we built the state space, a point of $T^*X$ is a pair $(q,p)$ with $q\in X$ and $p$ a covector at $q$. So there is a natural “forgetful” map that just returns the base point: $\pi(q,p)=q$. In the case $T^*S^1\cong S^1\times\mathbb{R}$, this is simply the first coordinate. ↩

2. Or how the state of the system evolves in time. ↩

3. The Poisson bracket is a way to define a Lie bracket on the space of functions on the state space. ↩

4. Interestingly, there are also higher degree variants or multi-symplectic structures $\omega \in \Omega^k(M)$ for $k \geq 2$. ↩